Neural Network Tricks
In this notebook, I’ll show the effects of various techniques (“tricks”) used to improve the performance of neural networks. Most of them come from the (LeCun, Bottou, Orr and Muller, 2012) paper.
Previously, we built a basic neural network in the “Backprop Exercise” notebook. Here, I’ll use a slightly refactored version of the NeuralNetwork class:
%pycat neural_network.pyfrom sklearn.decomposition import PCA
from sklearn.cross_validation import train_test_split, ShuffleSplit
from sklearn.preprocessing import OneHotEncoder
from neural_network import NeuralNetwork
# The classifier network
class ClassifierNetwork(NeuralNetwork):
"""Neural network with classification error plots."""
def errors_for(self, t, x):
x, t = self.preprocessed(x, t)
y = self.predictions_for(x)
mse = multiply(y-t,y-t).mean()
mce = (y.argmax(axis=1) != t.argmax(axis=1)).mean()
return mse, mce
def train_classifier(self, dataset, fig=None, ax=None, epochs=1000):
"""Perform the classification task for the data using the given network, without using train-test split."""
X, T = dataset.data, dataset.target
_X, _T = self.preprocessed(X, T)
errors=[]
for epoch in range(epochs):
self.update_weights(_T, _X)
errors.append(self.errors_for(T, X))
if fig is not None and mod(epoch+1, 100) == 0:
aerrors=array(errors).T
self.plot_errors(ax, aerrors.T, epoch, epochs, ylabel='Errors', ylim=3.0)
ax.legend(['RMSE', 'RMCE'], loc='ba')
clear_output(wait=True)
display(fig)
ax.cla()
if errors[-1][1] == 0: # Perfect classification
break
plt.close()
return errors[-1]
def plot_errors(self, ax, errors, epoch, epochs, ylabel, ylim=1.0):
"""Plots the error graph."""
ax.plot(arange(epoch), errors[:epoch])
ax.set_xlim([0, epochs])
ax.set_ylim([0, ylim])
ax.set_xlabel("Training epoch")
ax.set_ylabel(ylabel)
ax.set_title(ylabel)
ax.grid()
ax.legend(['Training', 'Test'], loc="best")
class ClassifierNetworkWithOneHot(ClassifierNetwork):
"""Encodes target values using one-hot encoding."""
def preprocessed(self, X, T=None):
if T is not None:
if not hasattr(self, 'encoder'):
self.encoder = OneHotEncoder(sparse=False).fit(T[:,newaxis])
T = self.encoder.transform(T[:,newaxis])*2 - 1
return super(ClassifierNetworkWithOneHot, self).preprocessed(X, T)
# Classifier with PCA preprocessing
class ClassifierNetworkForImages(ClassifierNetworkWithOneHot):
"""Applies PCA to the input data."""
def preprocessed(self, X, T=None):
if not hasattr(self, 'pca'):
self.pca = PCA(n_components = self.num_nodes[0], whiten=True, copy=True).fit(X)
return super(ClassifierNetworkForImages, self).preprocessed(self.pca.transform(X),T)
def train_classifier(self, dataset, fig=None, axs=None, epochs=1000, batch_size=0.1, test_size=0.2):
"""Perform the classification task for the data using the given network."""
# Split to training and test
X_train, X_test, T_train, T_test = train_test_split(dataset.data, dataset.target, test_size=test_size)
errors=[]
for epoch, epochs in self.train(X_train, T_train, epochs=epochs, batch_size=batch_size):
errors.append(self.errors_for(T_train, X_train) + self.errors_for(T_test, X_test))
if fig is not None and mod(epoch+1, 100) == 0:
aerrors=array(errors).T
self.plot_errors(axs[0], aerrors[::2].T, epoch, epochs, ylabel='RMSE', ylim=3.0)
self.plot_errors(axs[1], aerrors[1::2].T,epoch, epochs, ylabel='Classification Error', ylim=1.0)
clear_output(wait=True)
display(fig)
[ax.cla() for ax in axs]
plt.close()
train_rmse, train_rce, test_rmse, test_rce = errors[-1]
return train_rmse, test_rmse, train_rce, test_rceHere are some datasets we’ll be using:
from sklearn.datasets.base import Bunch
from sklearn.datasets import load_digits
# The XOR dataset
dataset_xor = Bunch()
dataset_xor['data'] = array([
[ 1,-1],
[-1, 1],
[ 1, 1],
[-1,-1]], dtype=float)
dataset_xor['target'] = array([
1,
1,
0,
0], dtype=float)
dataset_digits=load_digits()Now let’s see how the “basic” network does for these tasks.
base_xor_net = ClassifierNetworkWithOneHot(num_nodes=[2, 2, 2])
print(base_xor_net.train_classifier(dataset_xor, *plt.subplots(figsize=(5,5)), epochs=500))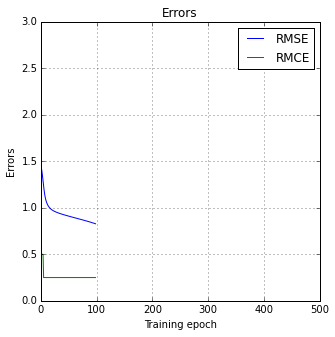
(0.43837751504121658, 0.0)
Note that the network often gets stuck in a local minimum.
base_digits_net = ClassifierNetworkForImages(num_nodes=[20, 20, 10])
print(base_digits_net.train_classifier(dataset_digits, *plt.subplots(1, 2, figsize=(10,5)), epochs=1000))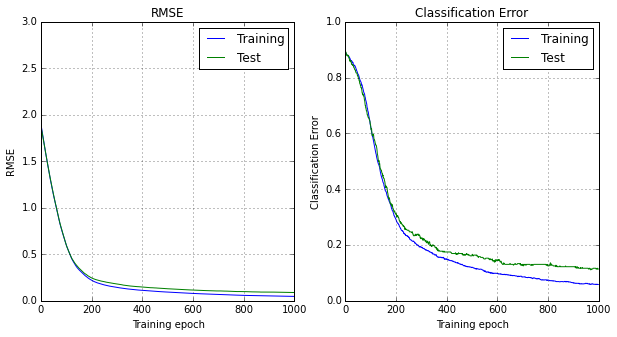
(0.047324129650683971, 0.088980205483812483, 0.05845511482254697, 0.11388888888888889)
Activation function
Let’s try the “funny tanh” as the activation function. For the XOR dataset, this ameliorates the problem of the network getting stuck in the local minimum.
from neural_network import ActivationFunction
class FunnyTanh(ActivationFunction):
def apply(self, x):
return 1.7159 * tanh(x*2/3) + 0.001 * x
funnytanh_xor_net = ClassifierNetworkWithOneHot(num_nodes=[2, 2, 2], activation_function=FunnyTanh())
# Train 10 times and see how many times it gets stuck
results=zeros((10,2))
epochs=300
for result in results:
Ws = base_xor_net.initial_weights() # keep the same initial weights
base_xor_net.Ws = Ws
funnytanh_xor_net.Ws = Ws
result[0]=base_xor_net.train_classifier(dataset_xor, epochs=epochs)[1]
result[1]=funnytanh_xor_net.train_classifier(dataset_xor, epochs=epochs)[1]
plt.bar(arange(2), (results<1e-8).mean(axis=0) * 100.0)
plt.xticks(arange(2)+.5, ['base', 'funnytanh'])
plt.xlim([-.25, 2.25])
plt.ylim([0, 100.0])
plt.grid()
plt.title('Pct successful training by %d epochs (out of %d trials)'% (epochs, results.shape[0]))
None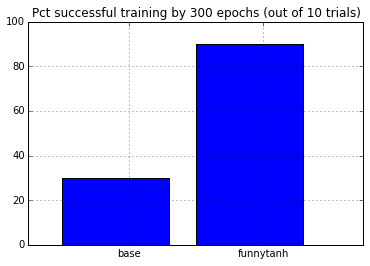
Better initial weights
Let’s change the initial random weights to have standard deviation of , where is the number of connection feeding into the node.
def better_initial_weights(self):
return [standard_normal((n + 1, m)) / sqrt(n + 1) for n, m in zip(self.num_nodes[:-1], self.num_nodes[1:])]
better_weight_xor_net = ClassifierNetworkWithOneHot(num_nodes=[2, 2, 2])
# Train 10 times and see how many times it gets stuck
results=zeros((10,2))
epochs=300
for result in results:
base_xor_net.Ws = base_xor_net.initial_weights()
better_weight_xor_net.Ws = better_initial_weights(better_weight_xor_net)
result[0]=base_xor_net.train_classifier(dataset_xor, epochs=epochs)[1]
result[1]=better_weight_xor_net.train_classifier(dataset_xor, epochs=epochs)[1]
plt.bar(arange(2), (results<1e-8).mean(axis=0) * 100.0)
plt.xticks(arange(2)+.5, ['base', 'better_weight'])
plt.xlim([-.25, 2.25])
plt.ylim([0, 100.0])
plt.grid()
plt.title('Pct successful training by %d epochs (out of %d trials)'% (epochs, results.shape[0]))
None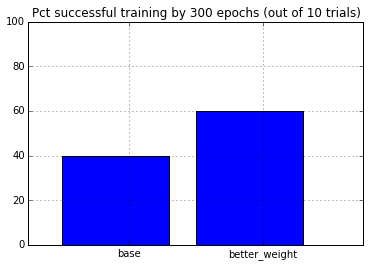
Momentum
Let’s add the momentum to the stochastic gradient update. Now, instead of updating the weights as
We will keep the previous weight update and momentum so that:
The momentum modulates how much of the previous weight update is reflected in the current update.
from neural_network import _with_bias
class ClassifierNetworkWithMomentum(ClassifierNetworkWithOneHot):
def __init__(self, *args, **kwargs):
super(ClassifierNetworkWithMomentum, self).__init__(*args, **kwargs)
self.momentum = kwargs['momentum'] if kwargs.has_key('momentum') else 0.9
self.Vs = [zeros(W.shape) for W in self.Ws]
def gradient_descent(self, deltas, zs):
N = zs[0].shape[0]
Js= [self.eta * dot(_with_bias(z).T, delta) / N for W, z, delta in zip(self.Ws, zs[:-1], deltas)]
self.Vs = [self.momentum * V - J for V, J in zip(self.Vs, Js)]
return [W + V for W, V in zip(self.Vs, self.Ws)]
momentum_xor_net = ClassifierNetworkWithMomentum(num_nodes=[2, 2, 2], eta=0.05)
#print(momentum_xor_net.train_classifier(dataset_xor, *plt.subplots(figsize=(5,5)), epochs=500))
# Train 10 times and see how many times it gets stuck
results=zeros((10,2))
epochs=600
for result in results:
Ws = base_xor_net.initial_weights()
base_xor_net.Ws = Ws
momentum_xor_net.Ws = Ws
result[0]=base_xor_net.train_classifier(dataset_xor, epochs=epochs)[1]
result[1]=momentum_xor_net.train_classifier(dataset_xor, epochs=epochs)[1]
plt.bar(arange(2), (results<1e-8).mean(axis=0) * 100.0)
plt.xticks(arange(2)+.5, ['base', 'momentum'])
plt.xlim([-.25, 2.25])
plt.ylim([0, 100.0])
plt.grid()
plt.title('Pct successful training by %d epochs (out of %d trials)'% (epochs, results.shape[0]))
None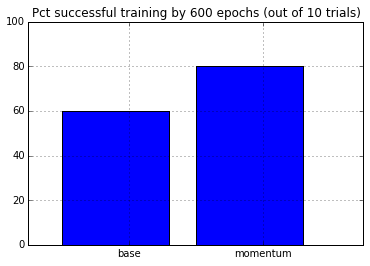
Pre-train using autoencoder
We’ll first perform an “unsupervised learning” using an auto-encoder: instead of predicting the target values, we’ll train it to predict the input values.
class AutoEncoderNetwork(ClassifierNetwork):
def train_unsupervised(self, dataset, fig=None, ax=None, epochs=1000):
"""Perform unsupervised learning from the data."""
X = self.preprocessed(dataset.data)
T = X.copy()
errors=[]
for epoch in range(epochs):
self.update_weights(T, X)
errors.append(self.errors_for(T, X))
if fig is not None and mod(epoch+1, 100) == 0:
aerrors=array(errors).T
self.plot_errors(ax, aerrors.T, epoch, epochs, ylabel='Errors', ylim=3.0)
ax.legend(['RMSE', '(Ignore this)'], loc='ba')
clear_output(wait=True)
display(fig)
ax.cla()
plt.close()
return errors[-1]
ae_xor_net = AutoEncoderNetwork(num_nodes=[2, 2, 2])
print(ae_xor_net.train_unsupervised(dataset_xor, *plt.subplots(figsize=(5,5)), epochs=500))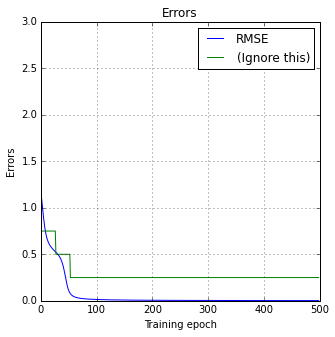
(0.0021059631785851855, 0.25)
Then, we’d train the classifier network starting from the hidden weights that was learned.
ae_xor_net = AutoEncoderNetwork(num_nodes=[2, 2, 2])
aeweight_xor_net = ClassifierNetworkWithOneHot(num_nodes=[2, 2, 2], activation_function=FunnyTanh())
# Train 10 times and see how many times it gets stuck
results=zeros((10,2))
epochs=300
for result in results:
Ws = base_xor_net.initial_weights()
base_xor_net.Ws = Ws
ae_xor_net.Ws = ae_xor_net.initial_weights()
ae_xor_net.train_unsupervised(dataset_xor, epochs=100) # Only train for a short amount
Wh = ae_xor_net.Ws[0]
aeweight_xor_net.Ws = [W.copy() for W in Ws]
aeweight_xor_net.Ws[0] = Wh
result[0]=base_xor_net.train_classifier(dataset_xor, epochs=epochs)[1]
result[1]=aeweight_xor_net.train_classifier(dataset_xor, epochs=epochs)[1]
plt.bar(arange(2), (results<1e-8).mean(axis=0) * 100.0)
plt.xticks(arange(2)+.5, ['base', 'autoencoder'])
plt.xlim([-.25, 2.25])
plt.ylim([0, 100.0])
plt.grid()
plt.title('Pct successful training by %d epochs (out of %d trials)'% (epochs, results.shape[0]))
None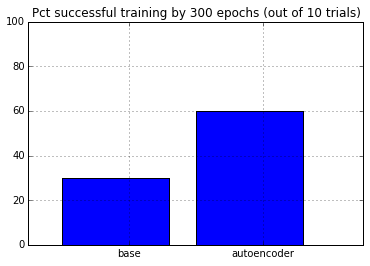
Putting everything together
Now we’ll combine all of the techniques above. We’ll also run it longer (1000 epochs) to see if
class ClassifierNetwork2(ClassifierNetworkWithMomentum):
def __init__(self, *args, **kwargs):
if not kwargs.has_key('activation_function'):
kwargs['activation_function'] = FunnyTanh()
super(ClassifierNetwork2, self).__init__(*args, **kwargs)
def initial_weights(self):
Ws0 = [standard_normal((n + 1, m)) / sqrt(n + 1) for n, m in zip(self.num_nodes[:-1], self.num_nodes[1:])]
ae_network = AutoEncoderNetwork(num_nodes=[self.num_nodes[0], self.num_nodes[1], self.num_nodes[0]],Ws = Ws0)
ae_network.train_unsupervised(dataset_xor, epochs=100) # Only train for a short amount
Ws0[0] = ae_network.Ws[0]
return Ws0
improved_xor_net = ClassifierNetwork2(num_nodes=[2, 2, 2], eta=0.05)
# Train 10 times and see how many times it gets stuck
results=zeros((10,2))
epochs=600
for result in results:
base_xor_net.Ws = base_xor_net.initial_weights()
improved_xor_net.Ws = improved_xor_net.initial_weights()
result[0]=base_xor_net.train_classifier(dataset_xor, epochs=epochs)[1]
result[1]=improved_xor_net.train_classifier(dataset_xor, epochs=epochs)[1]
plt.bar(arange(2), (results<1e-8).mean(axis=0) * 100.0)
plt.xticks(arange(2)+.5, ['base', 'improved'])
plt.xlim([-.25, 2.25])
plt.ylim([0, 100.0])
plt.grid()
plt.title('Pct successful training by %d epochs (out of %d trials)'% (epochs, results.shape[0]))
None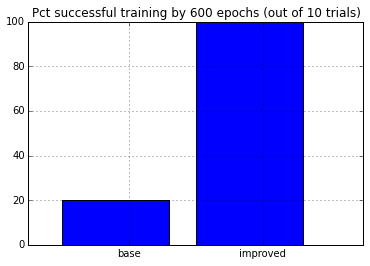
#References
[^](#ref-1) LeCun, Yann A and Bottou, Leon and Orr, Genevieve B and Muller, Klaus-Robert. 2012. Efficient backprop.